Xixihe Railway Bridge
Xixihe Railway Bridge
成贵高铁西溪河大桥
Dafang, Guizhou, China
840 feet high / 256 meters high
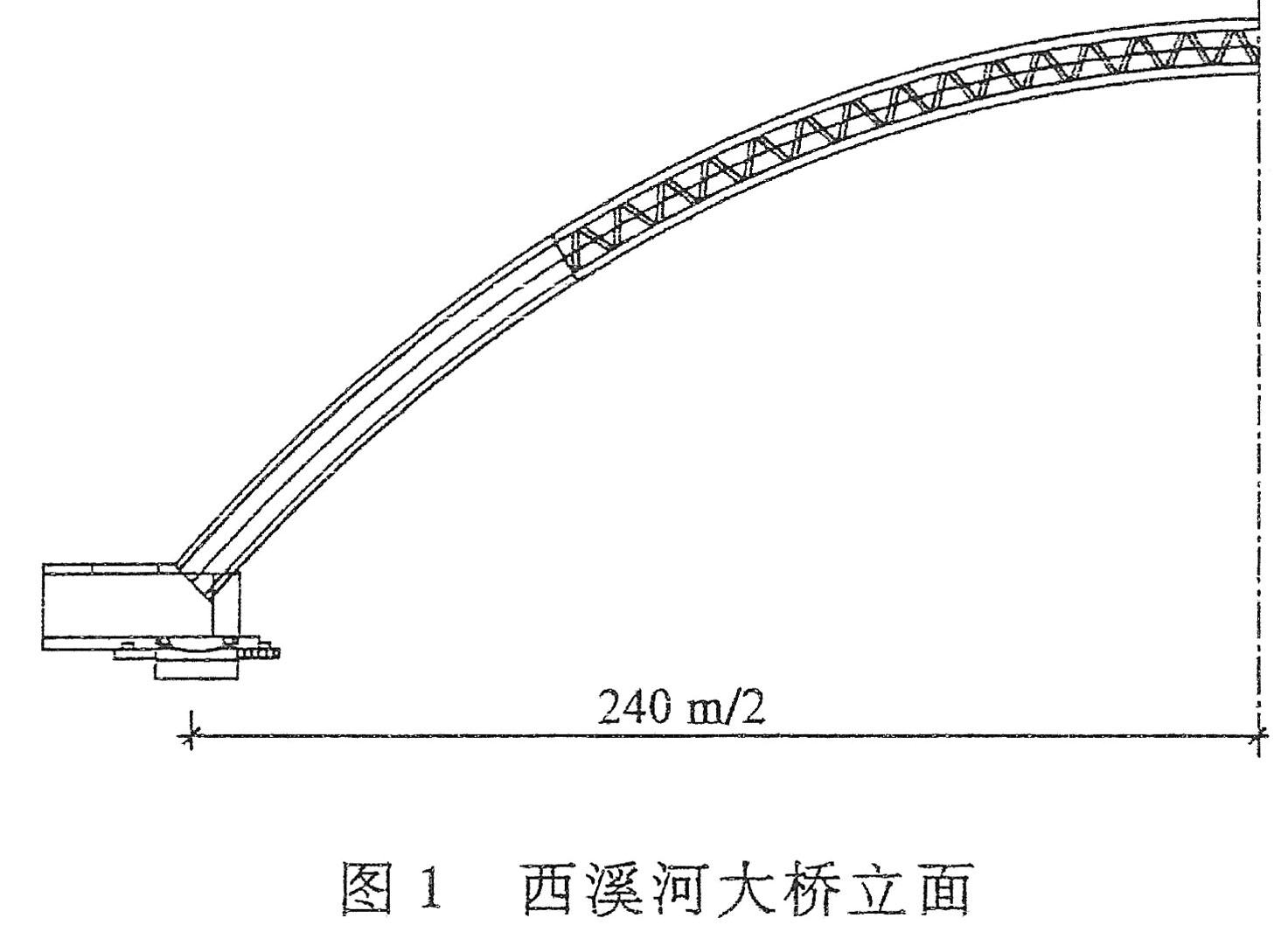
787 foot span / 240 meter span
2019
One of the highest railway spans in the world, the Xixihe Railway Bridge is one of many breathtaking bridges on the high speed, twin track railway line between Guiyang and Chengdu. The Xixi River crossing is very similar in size to the famous Beipanjiang Railway Bridge Shuibai and has a similar steel arch with a span of 240 meters. The lower half of the canyon consists of nearly vertical cliffs that allow little sunlight to reach the river.
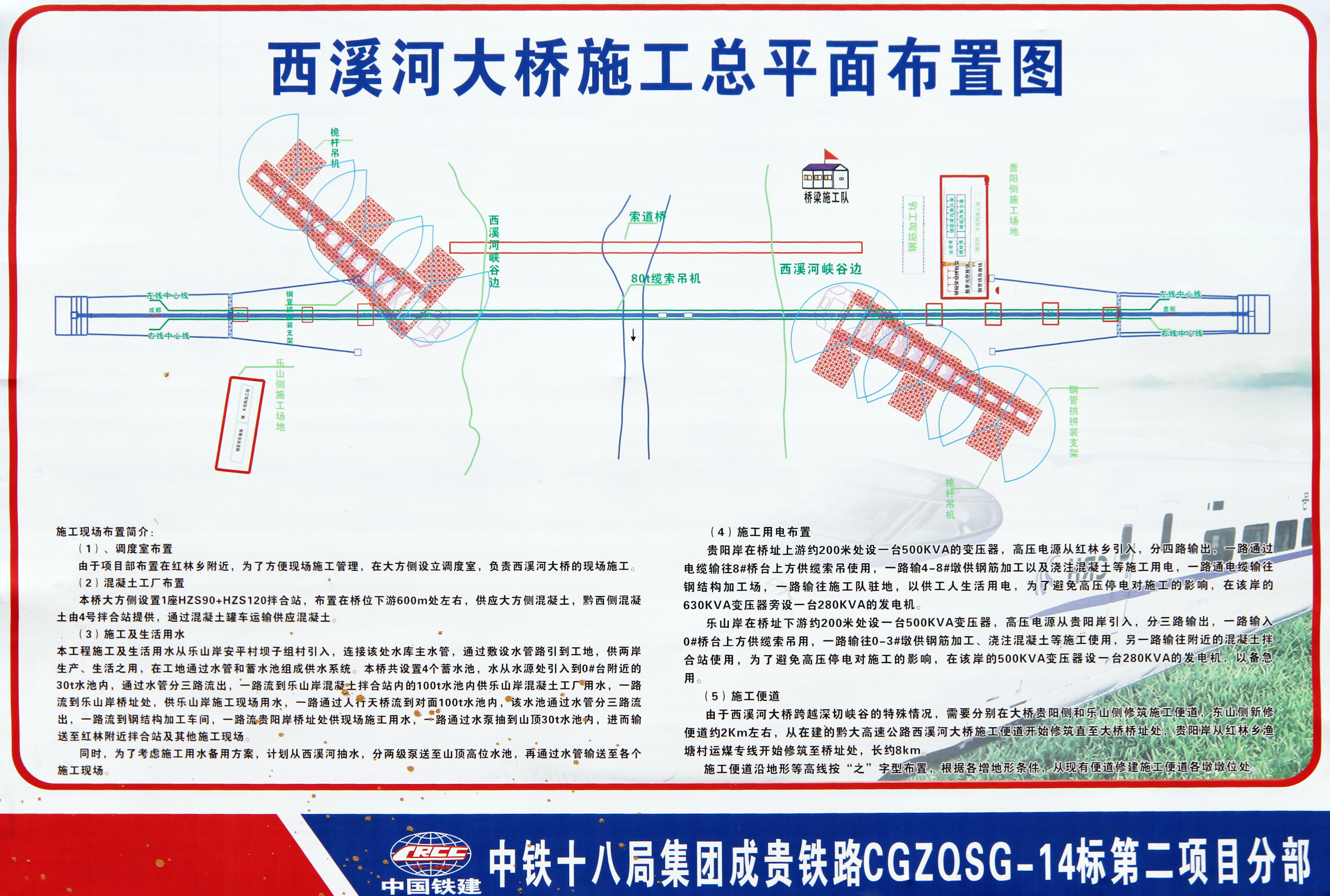
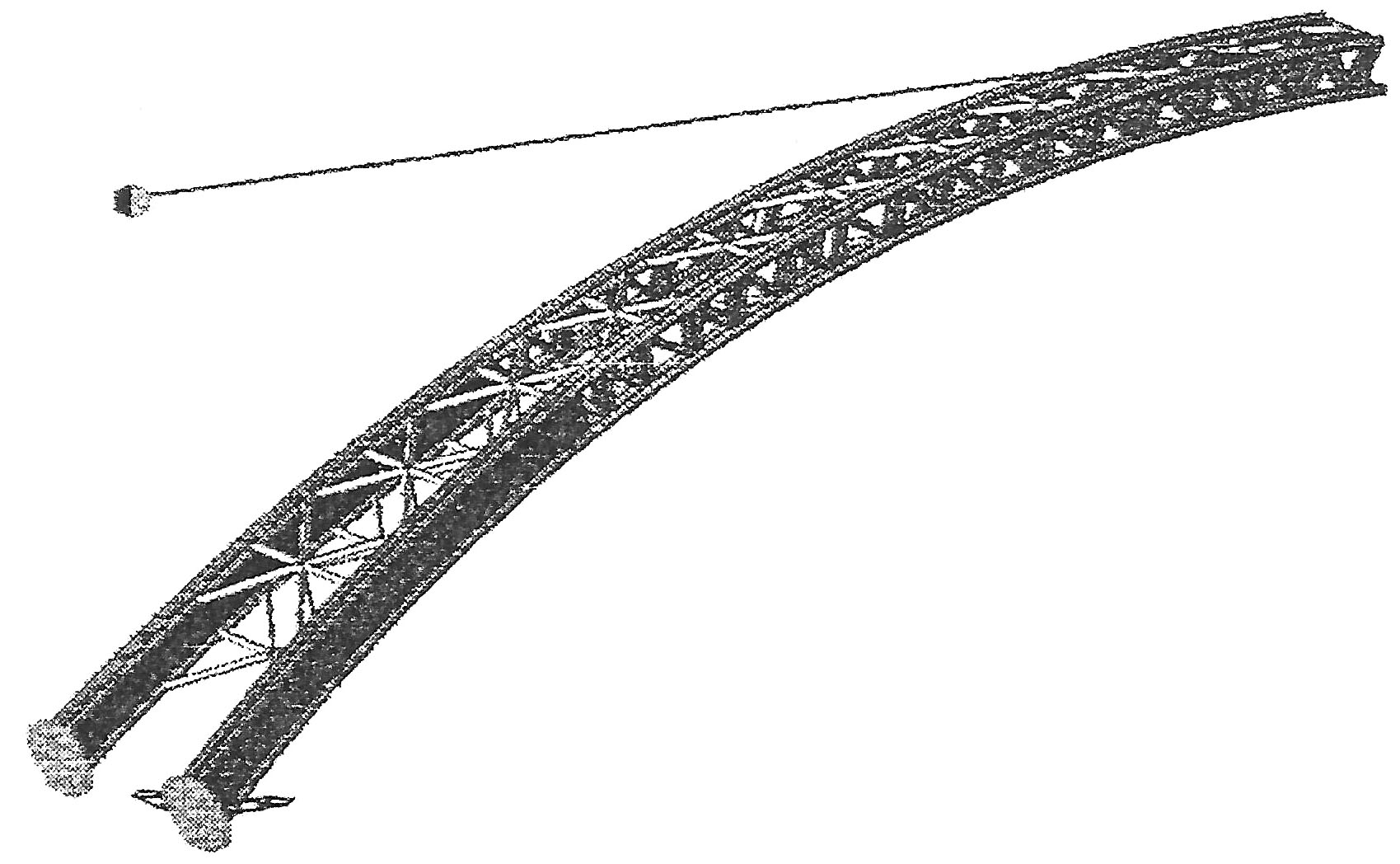
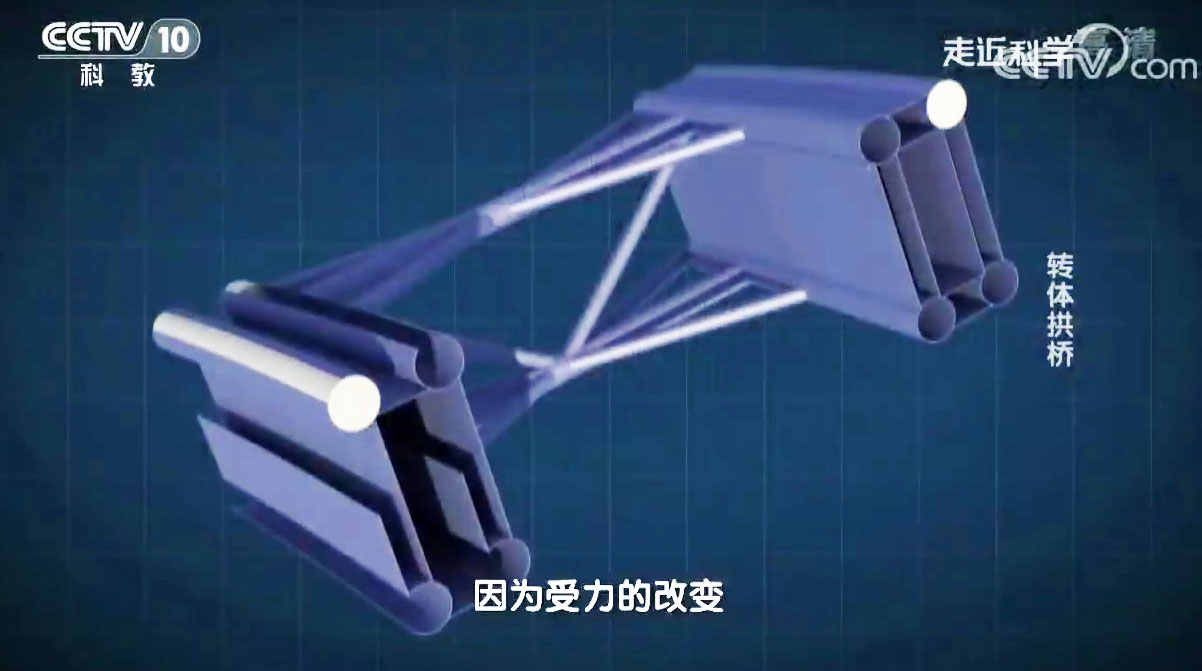
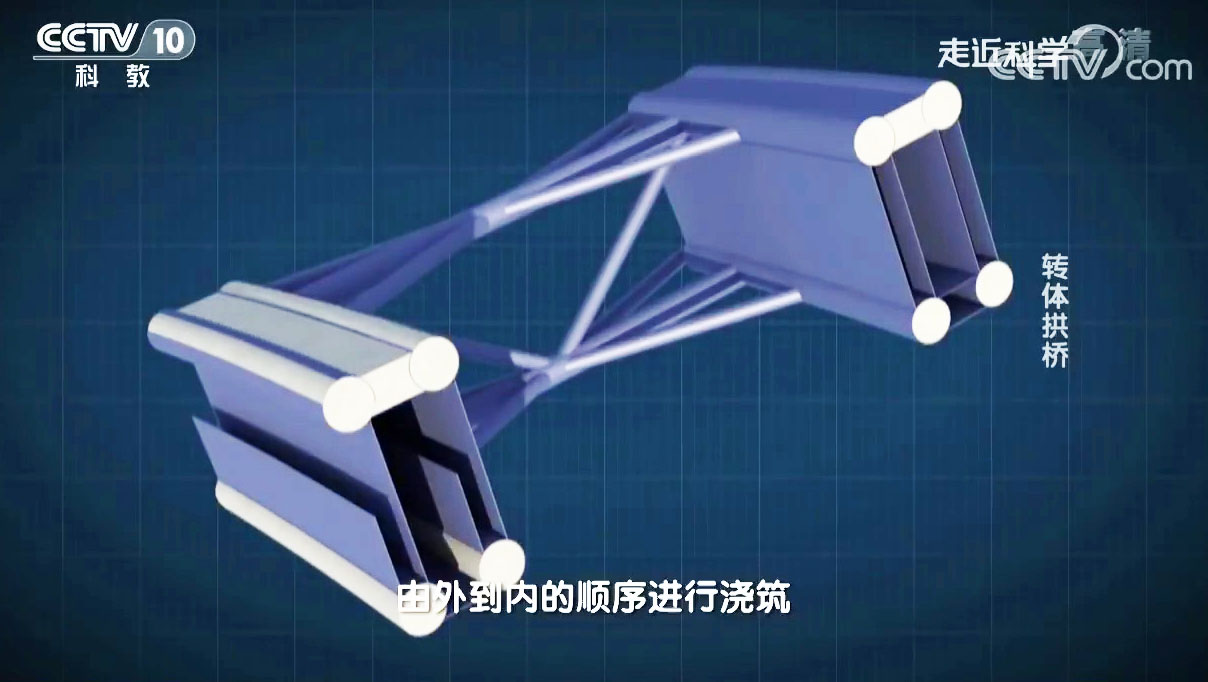
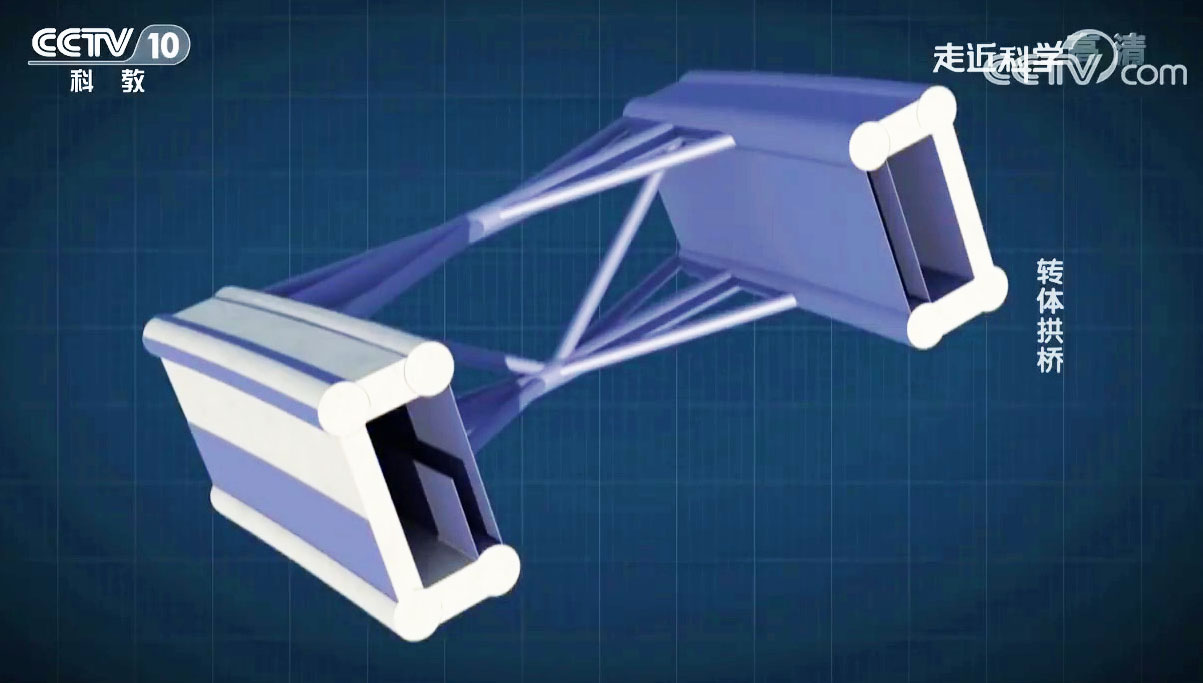
Construction of the Xixihe Railway was built using a method developed by the Chinese that has only been used on a gorge crossing once before on the Beipanjiang Bridge Shuibai. Instead of building two temporary towers to support a “high line” to assist in building the two sides of the arch outward until they met in the middle, the two halves of the bridge were built separately on falsework constructed just above ground on the hillsides at the edge of the canyon. Once completed, each side was then rotated horizontally outward over the river in one delicate maneuver and then connected at the crown. The central bearing located on top of each of the foundations used teflon to keep friction to a minimum. A massive water tank was installed on the back of the counter weighting pier to assist in finding an accurate center of gravity as well as preventing the system from overturning. Once the two halves of the arch were closed at the crown, the rotatable foundations were entombed in tons of concrete. This unique method of rotating the arch halves during construction has been used on other large arch bridges in China including those that are built on flat terrain just above the level of the river.
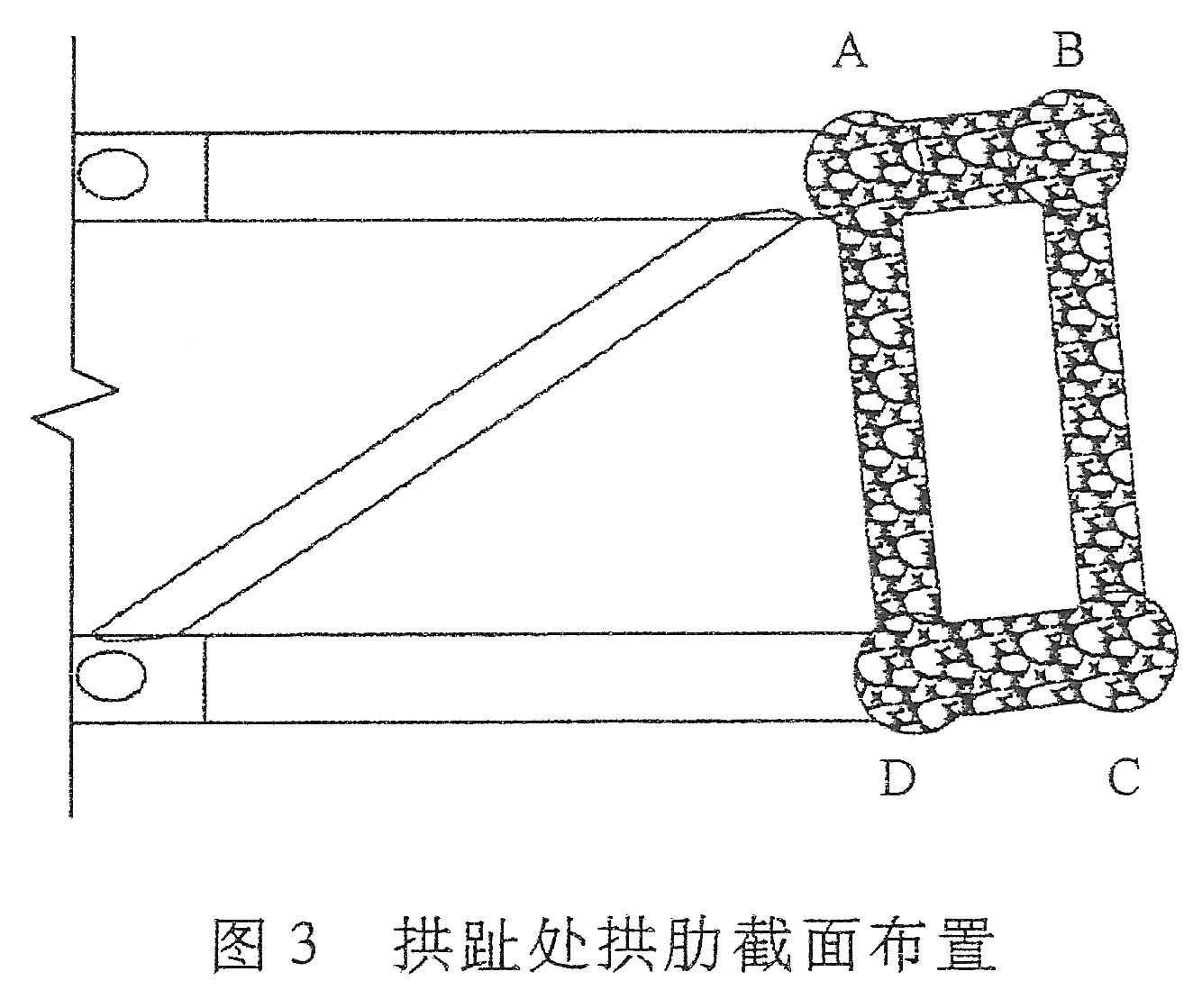
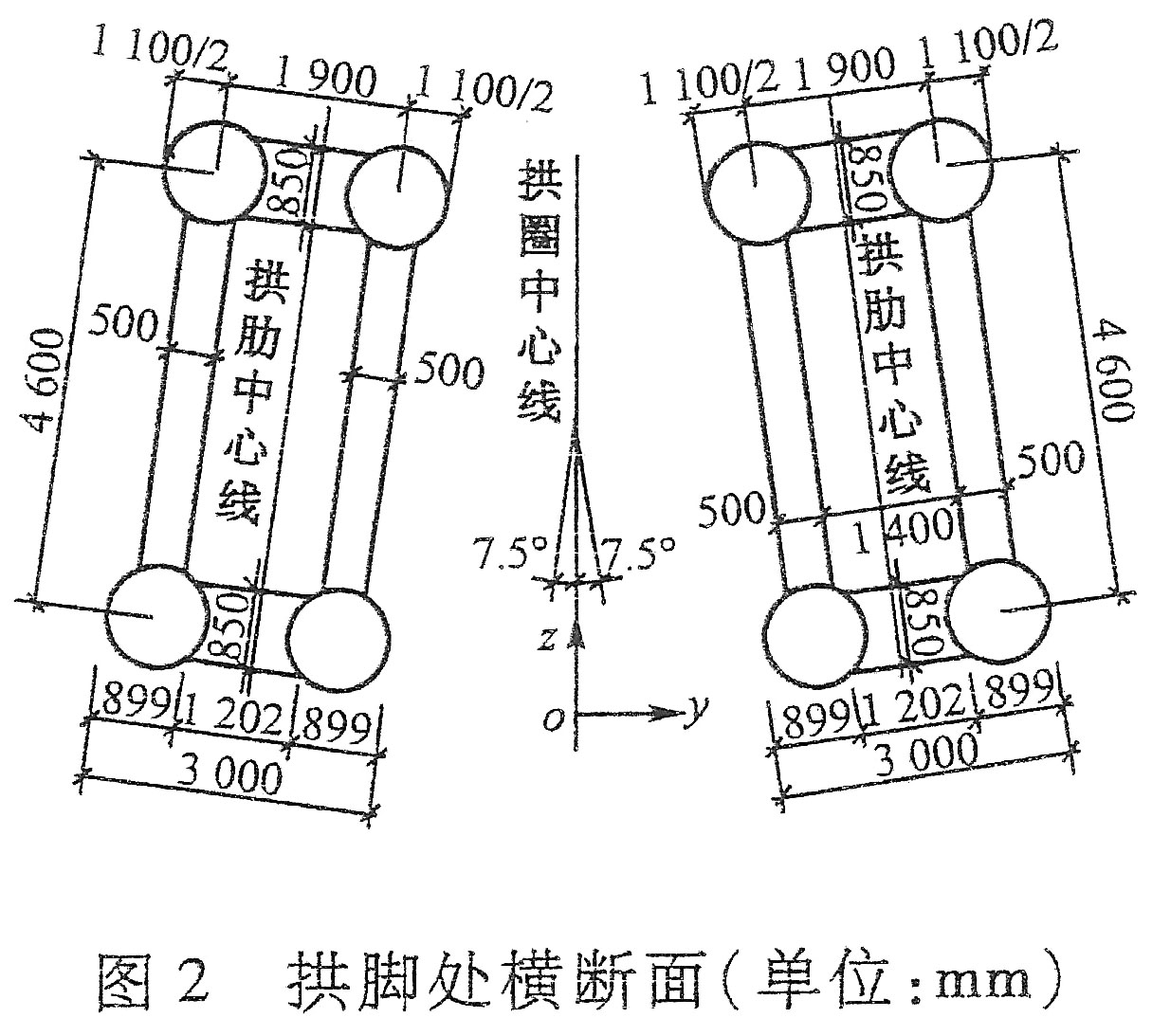
The two steel arch ribs on the Xixihe Railway Bridge were initially hollow during construction before concrete was pumped inside of them from the foundations upward to the crown. First used by the Chinese in 1990, they have refined and improved the technique and now use it on the majority of their steel arch bridges. Depending on the length of the span and the width of the bridge, different styles of tubing are used. For the Xixihe, a mix of a horizontal dumbbell and single tubes was adopted. Other configurations have single tubes further apart, double dumbbells or a tight cluster of tubes known as “multiple contiguous”. Once hardened, the concrete solidifies and stiffens the arch, improving the compressive strength of the entire structure.
The tight canyon resulted in a relatively short bridge length of just 493.6 meters consisting of a span arrangement of 3x32.7 +240+ 4x32.7 meters.
A dam was completed 1 kilometer downstream of the Xixihe Railway Bridge that created a reservoir beneath the crossing in 2024.
Image by Eric Sakowski.
Image by Eric Sakowski.
Image by Ben Usagani.
Image by Eric Sakowski.
Image by Ben Usagani.
Image by Eric Sakowski.
Image by Eric Sakowski.
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Image by Eric Sakowski / HighestBridges.com
Xixihe Railway Bridge headquarters. Image by Eric Sakowski / HighestBridges.com
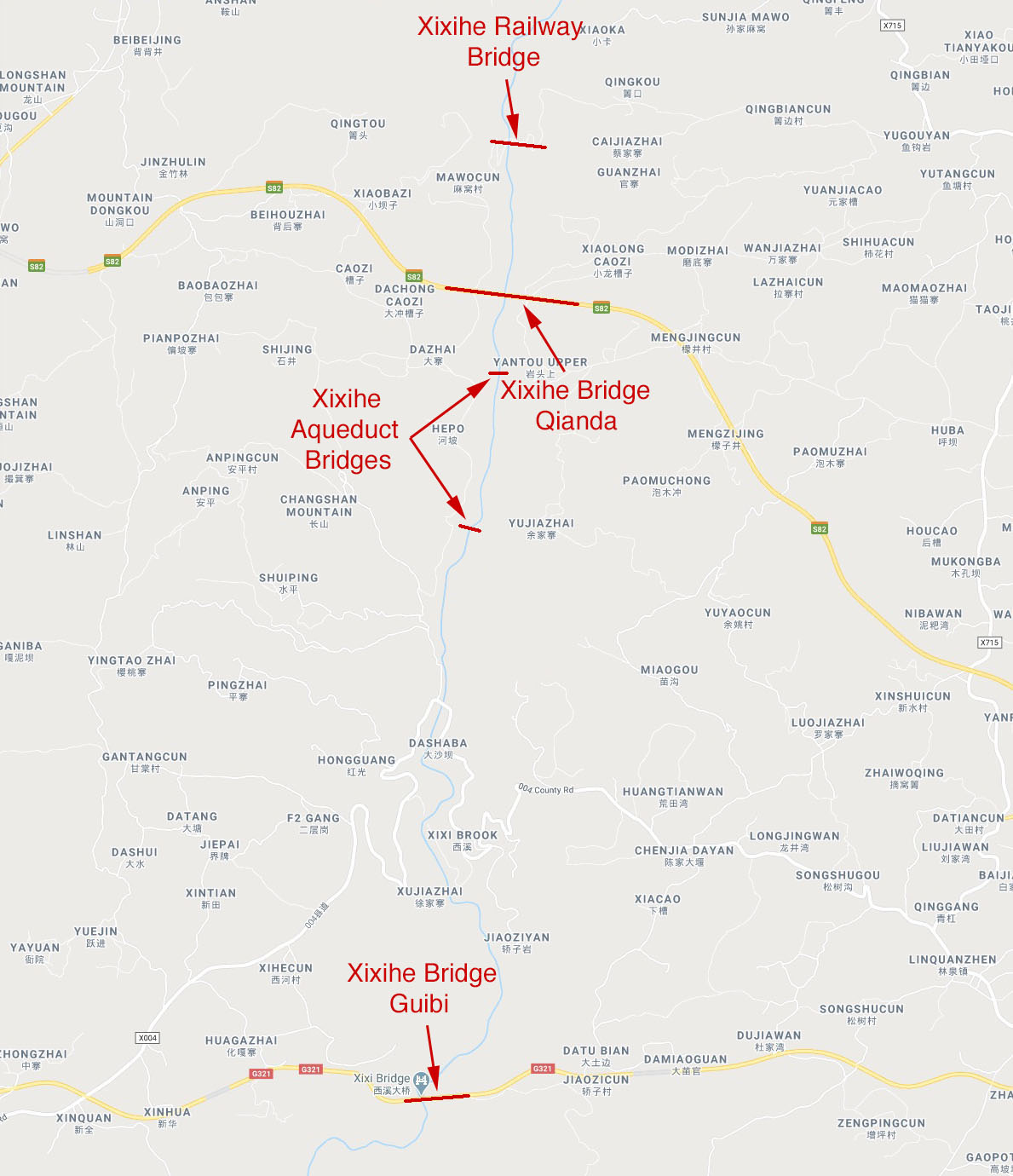
Xixihe Railway Bridge Satellite image.
Xixihe Satellite image showing the Railway Bridge to the North and the expressway bridge to the South.
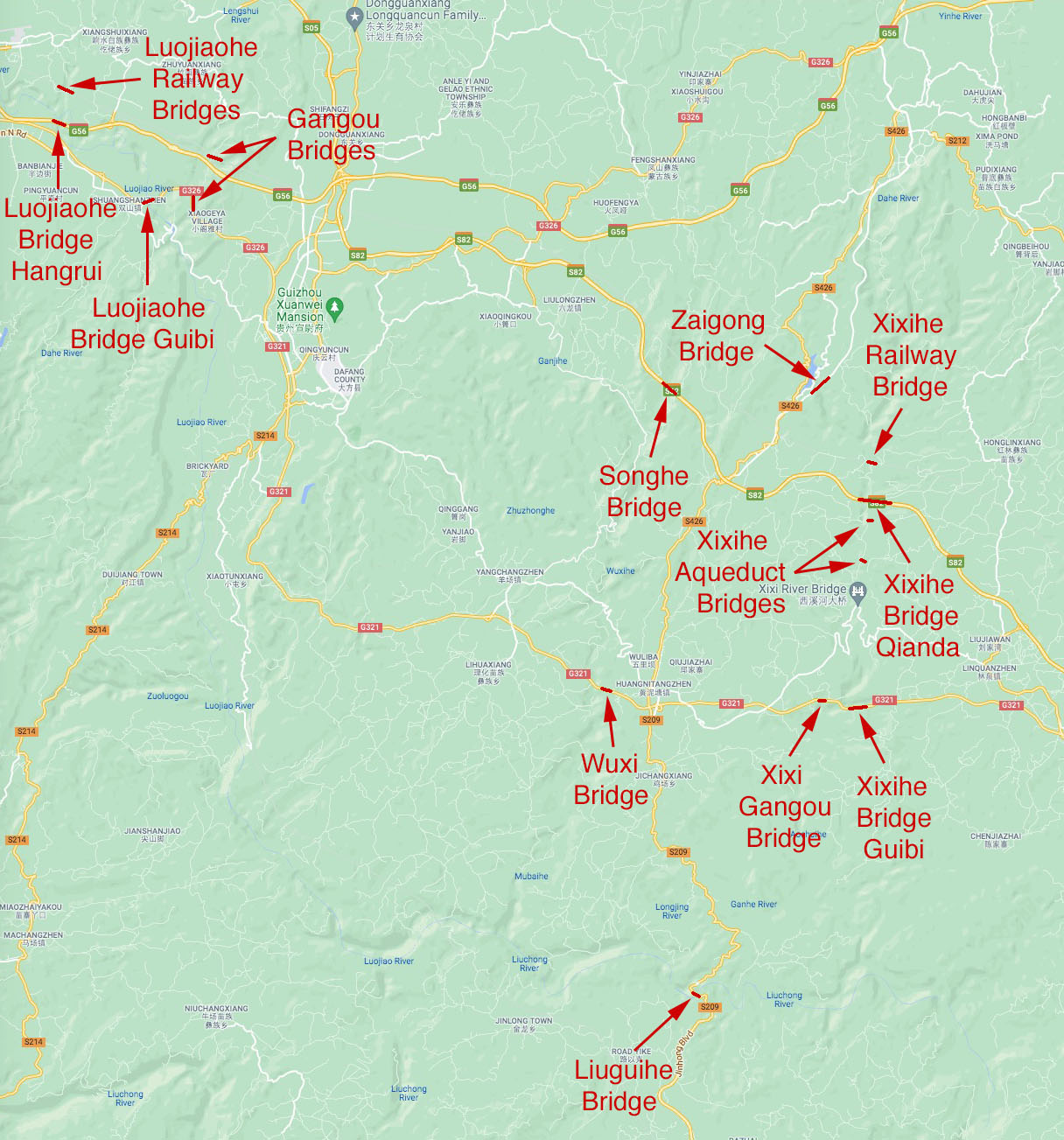
Xixihe Railway Bridge location map.
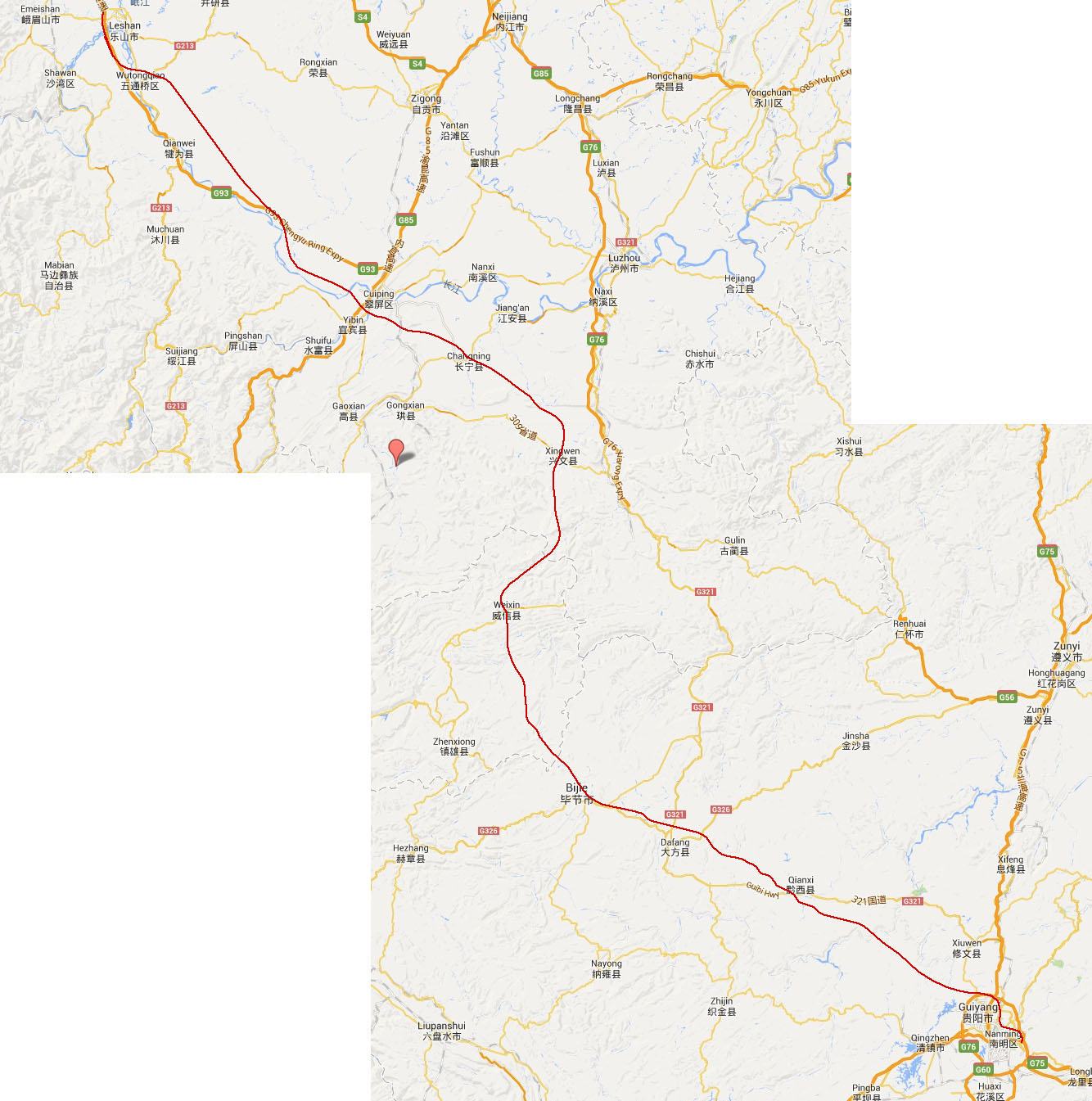
Chengdu-Guiyang Railway map.